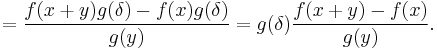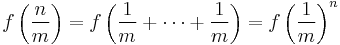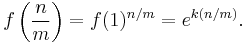Characterizations of the exponential function
In mathematics, the exponential function can be characterized in many ways. The following characterizations (definitions) are most common. This article discusses why each characterization makes sense, and why the characterizations are independent of and equivalent to each other. As a special case of these considerations, we will see that the three most common definitions given for the mathematical constant e are also equivalent to each other.
Contents |
Characterizations
The five most common definitions of the exponential function exp(x) = ex for real x are:
- 1. Define ex by the limit
- 2. Define ex as the value of the infinite series
-
- (Here n! stands for the factorial of n. One proof that e is irrational uses this representation.)
- 3. Define ex to be the unique number y > 0 such that
-
-
- This is as the inverse of the natural logarithm function, which is defined by this integral.
-
- 4. Define ex to be the unique solution to the initial value problem
- 5. The exponential function f(x) = ex is the unique Lebesgue-measurable function with f(1) = e that satisfies
-
- (Hewitt and Stromberg, 1965, exercise 18.46). Alternatively, it is the unique anywhere-continuous function with these properties (Rudin, 1976, chapter 8, exercise 6).
- (As a counterexample, if one does not assume continuity or measurability, it is possible to prove the existence of an everywhere-discontinuous, non-measurable function with this property by using a Hamel basis for the real numbers over the rationals, as described in Hewitt and Stromberg.)
- Because f(x) = ex is guaranteed for rational x by the above properties (see below), one could also use monotonicity or other properties to enforce the choice of ex for irrational x, but such alternatives appear to be uncommon.
-
Larger domains
One way of defining the exponential function for domains larger than the domain of real numbers is to first define it for the domain of real numbers using one of the above characterizations and then extend it to larger domains in a way which would work for any analytic function.
It is also possible to use the characterisations directly for the larger domain, though some problems may arise. (1), (2), and (4) all make sense for arbitrary Banach algebras. (3) presents a problem for complex numbers, because there are non-equivalent paths along which one could integrate, and (5) is not sufficient. For example, the function f defined (for x and y real) as
satisfies the conditions in (5) without being the exponential function of x + iy. To make (5) sufficient for the domain of complex numbers, one may either stipulate that there exists a point at which f is a conformal map or else stipulate that
Why each characterization makes sense
Each characterization requires some justification to show that it makes sense. For instance, when the value of the function is defined by a sequence or series, the convergence of this sequence or series needs to be established.
Characterization 2
Since
it follows from the ratio test that 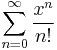 converges for all x.
converges for all x.
Characterization 3
Since the integrand is an integrable function of t, the integral expression makes sense. That every real number x corresponds to a unique y > 0 such that
is equivalent to the statement that the integral is a bijection from the interval 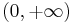 to
to 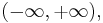 which follows if one can show that 1/t is positive for positive t (so the function is monotone increasing, hence one-to-one) and that the two integrals
which follows if one can show that 1/t is positive for positive t (so the function is monotone increasing, hence one-to-one) and that the two integrals
hold, so it is onto.
The first statement is obvious – 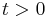 implies
implies 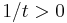 – and the two integrals follow from the integral test and the divergence of the harmonic series.
– and the two integrals follow from the integral test and the divergence of the harmonic series.
Equivalence of the characterizations
The following proof demonstrates the equivalence of the three characterizations given for e above. The proof consists of two parts. First, the equivalence of characterizations 1 and 2 is established, and then the equivalence of characterizations 1 and 3 is established.
Equivalence of characterizations 1 and 2
The following argument is adapted from a proof in Rudin, theorem 3.31, p. 63-65.
Let 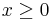 be a fixed non-negative real number. Define
be a fixed non-negative real number. Define
By the binomial theorem,
(using x ≥ 0 to obtain the final inequality) so that
where ex is in the sense of definition 2. Here, we must use limsups, because we don't yet know that tn actually converges. Now, for the other direction, note that by the above expression of tn, if 2 ≤ m ≤ n, we have
Fix m, and let n approach infinity. We get
(again, we must use liminf's because we don't yet know that tn converges). Now, take the above inequality, let m approach infinity, and put it together with the other inequality. This becomes
so that
We can then extend this equivalence to the negative real numbers by noting 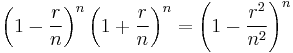 and taking the limit as n goes to infinity.
and taking the limit as n goes to infinity.
The error term of this limit-expression is described by
where the polynomial's degree (in x) in the term with denominator nk is 2k.
Equivalence of characterizations 1 and 3
Here, we define the natural logarithm function in terms of a definite integral as above. By the fundamental theorem of calculus,
Now, let x be any fixed real number, and let
We will show that ln(y) = x, which implies that y = ex, where ex is in the sense of definition 3. We have
Here, we have used the continuity of ln(y), which follows from the continuity of 1/t:
Here, we have used the result lnan = nlna. This result can be established for n a natural number by induction, or using integration by substitution. (The extension to real powers must wait until ln and exp have been established as inverses of each other, so that ab can be defined for real b as eb lna.)
Equivalence of characterizations 1 and 5
The following proof is a simplified version of the one in Hewitt and Stromberg, exercise 18.46. First, one proves that measurability (or here, Lebesgue-integrability) implies continuity for a non-zero function  satisfying
satisfying  , and then one proves that continuity implies
, and then one proves that continuity implies 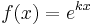 for some k, and finally
for some k, and finally 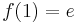 implies k=1.
implies k=1.
First, we prove a few elementary properties from  satisfying
satisfying  and the assumption that
and the assumption that  is not identically zero:
is not identically zero:
- If
 is nonzero anywhere (say at x=y), then it is non-zero everywhere. Proof:
is nonzero anywhere (say at x=y), then it is non-zero everywhere. Proof: 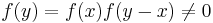 implies
implies 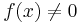 .
. 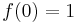 . Proof:
. Proof: 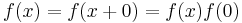 and
and  is non-zero.
is non-zero. . Proof:
. Proof: 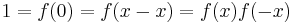 .
.- If
 is continuous anywhere (say at x=y), then it is continuous everywhere. Proof:
is continuous anywhere (say at x=y), then it is continuous everywhere. Proof: ![f(x%2B\delta)-f(x) = f(x-y) [ f(y%2B\delta) - f(y)] \rightarrow 0](/2012-wikipedia_en_all_nopic_01_2012/I/9f8d7c2fb020bb8ff0a677b5d3fe2e53.png) as
as 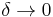 by continuity at y.
by continuity at y.
The second and third properties mean that it is sufficient to prove 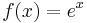 for positive x.
for positive x.
If  is a Lebesgue-integrable function, then we can define
is a Lebesgue-integrable function, then we can define
It then follows that
Since  is nonzero, we can choose some y such that
is nonzero, we can choose some y such that 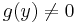 and solve for
and solve for  in the above expression. Therefore:
in the above expression. Therefore:
The final expression must go to zero as 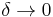 since
since 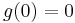 and
and 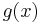 is continuous. It follows that
is continuous. It follows that  is continuous.
is continuous.
Now, we prove that 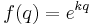 , for some k, for all positive rational numbers q. Let q=n/m for positive integers n and m. Then
, for some k, for all positive rational numbers q. Let q=n/m for positive integers n and m. Then
by elementary induction on n. Therefore, 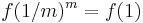 and thus
and thus
for ![k = \ln [f(1)]\,](/2012-wikipedia_en_all_nopic_01_2012/I/a1bf0ab0344d08d4eeb4add38919f376.png) . Note that if we are restricting ourselves to real-valued
. Note that if we are restricting ourselves to real-valued  , then
, then 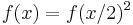 is everywhere positive and so k is real.
is everywhere positive and so k is real.
Finally, by continuity, since 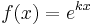 for all rational x, it must be true for all real x since the closure of the rationals is the reals (that is, we can write any real x as the limit of a sequence of rationals). If
for all rational x, it must be true for all real x since the closure of the rationals is the reals (that is, we can write any real x as the limit of a sequence of rationals). If 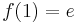 then k = 1. This is equivalent to characterization 1 (or 2, or 3), depending on which equivalent definition of e one uses.
then k = 1. This is equivalent to characterization 1 (or 2, or 3), depending on which equivalent definition of e one uses.
References
- Walter Rudin, Principles of Mathematical Analysis, 3rd edition (McGraw-Hill, 1976), chapter 8.
- Edwin Hewitt and Karl Stromberg, Real and Abstract Analysis (Springer, 1965).
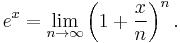
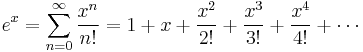
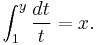
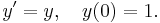
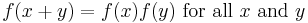
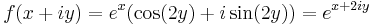
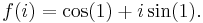
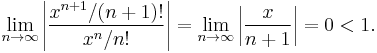
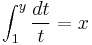
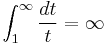
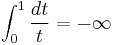
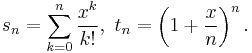
![\begin{align}
t_n & =\sum_{k=0}^n{n \choose k}\frac{x^k}{n^k}=1%2Bx%2B\sum_{k=2}^n\frac{n(n-1)(n-2)\cdots(n-(k-1))x^k}{k!\,n^k} \\[8pt]
& = 1%2Bx%2B\frac{x^2}{2!}\left(1-\frac{1}{n}\right)%2B\frac{x^3}{3!}\left(1-\frac{1}{n}\right)\left(1-\frac{2}{n}\right)%2B\cdots \\[8pt]
& {}\qquad \cdots %2B\frac{x^n}{n!}\left(1-\frac{1}{n}\right)\cdots\left(1-\frac{n-1}{n}\right)\le s_n
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/2650d4009fba0f00654506b0df27db58.png)
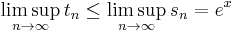
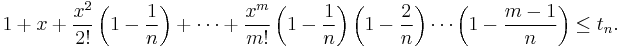
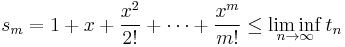
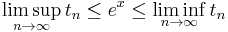
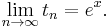
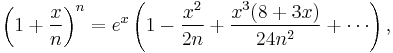
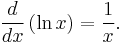
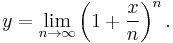
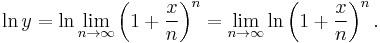
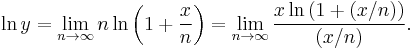
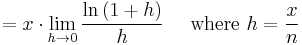
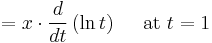
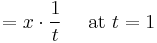
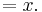
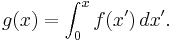
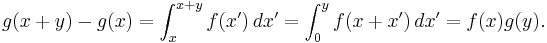
![f(x%2B\delta)-f(x) = \frac{[g(x%2B\delta%2By)-g(x%2B\delta)]-[g(x%2By)-g(x)]}{g(y)}](/2012-wikipedia_en_all_nopic_01_2012/I/156773c376e1280c91cfbe73b34c34bf.png)
![=\frac{[g(x%2By%2B\delta)-g(x%2By)]-[g(x%2B\delta)-g(x)]}{g(y)}](/2012-wikipedia_en_all_nopic_01_2012/I/9d57a71442338360925ea8acc59e60c1.png)